三角関数の学習に入る前段階として、三平方の定理と有名三角形の知識を再確認することは非常に重要です。これらは、三角比の定義や値の計算、各種公式の導出といった学習の土台となる内容です。特に「辺の長さの比」を正確に扱えるかどうかは、その後の理解度に大きく影響します。
授業では、生徒の反応を観察しながら、必要に応じて繰り返し確認して定着を図ります。
三平方の定理の確認

直角三角形に成り立つのは、何の定理でしたか?

三平方の定理です!

その通り!どんな式が作れますか?

\( a^2+b^2=c^2 \) です。
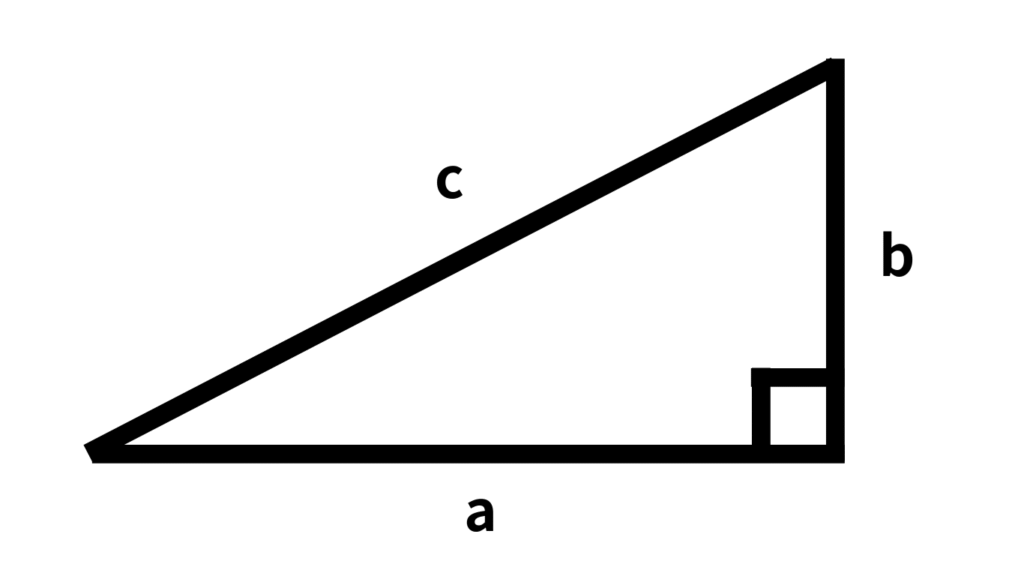
【三平方の定理】
辺の長さをa,b,斜辺の長さをcとする直角三角形において
\[a^2+b^2=c^2 \]
が成り立つ。平方数は2乗した数って意味だから、3つの平方数の成り立つ式のことでしたね。
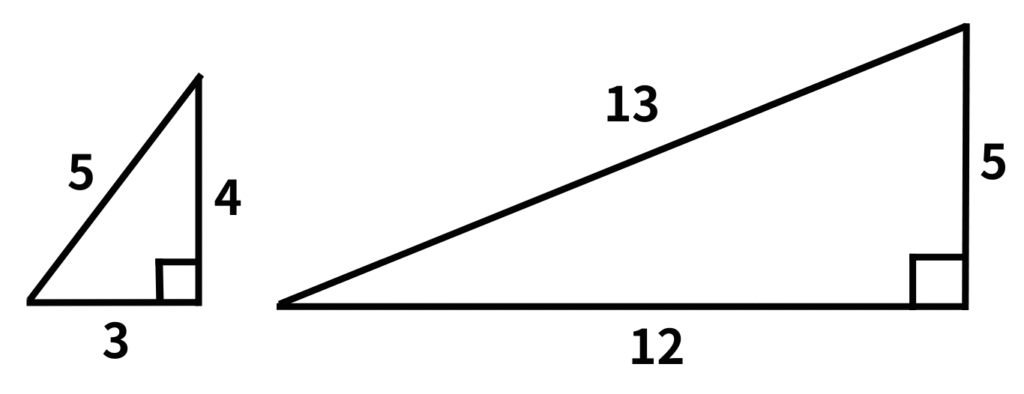
三平方の定理\( a^2+b^2=c^2 \)が成り立つ自然数の組\( (a, b, c) \)をピタゴラス数といいます。1つの三角比から他の三角比を求める問題は頻出なので、この2組のピタゴラス数は確実に確認しておきましょう。
有名三角形の確認
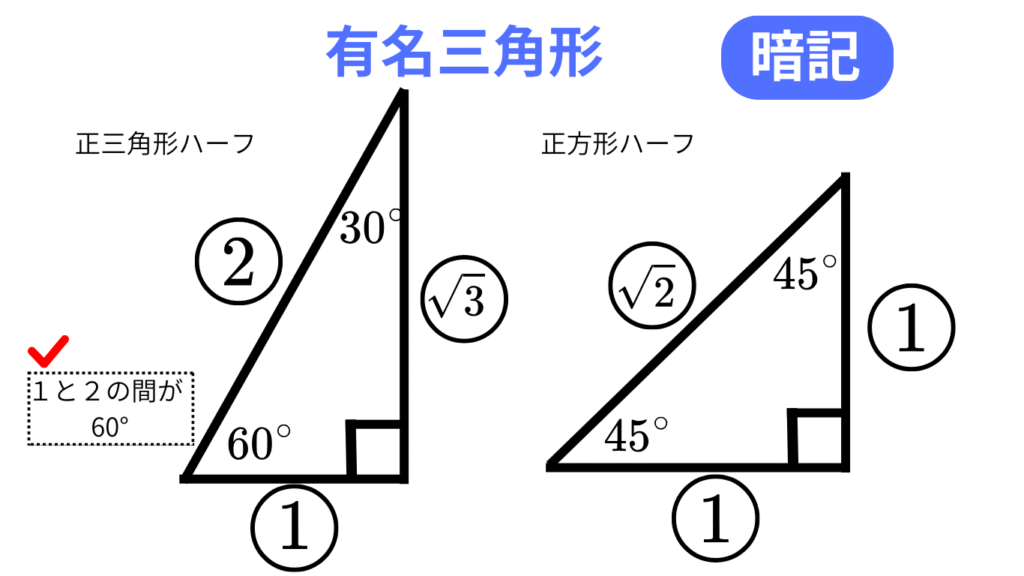
直角三角形のうち 30°–60°–90° と 45°–45°–90° を「有名三角形」と呼んで扱います。どちらも小学校から三角定規で慣れ親しんだ形であり、三角関数の学習には必要不可欠です。図を提示したら、まず 辺の比 と 角度 を確認します。
- 30°–60°–90°:辺の比は 1 : √3 : 2(正三角形ハーフ)
- 45°–45°–90°:辺の比は 1 : 1 : √2(正方形ハーフ)
特に混乱しやすいのは 30° と 60° の位置です。合言葉として
「1 と 2 の間が 60°」(= 長さ1と2の辺がつく角が60°)
を共有すると定着が良くなります。あわせて「最短の辺の向かいが 30°」と押さえると、向きが変わっても判断できます。
ひっかけ問題で記憶の定着
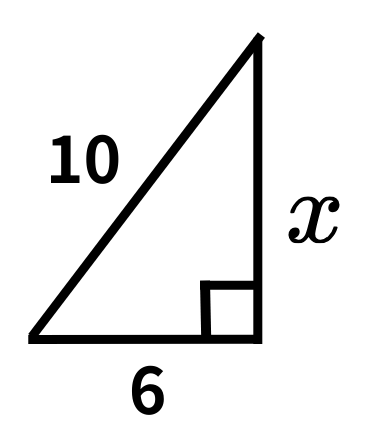

\( x \)を求めるのは、どうしますか?

\( 6^2+x^2=10^2 \) だから、……

ピタゴラス数(3, 4, 5)の2倍だと考えると、すぐに求めることができますね。

なるほど。\( x=8 \) って暗算で出せますね。
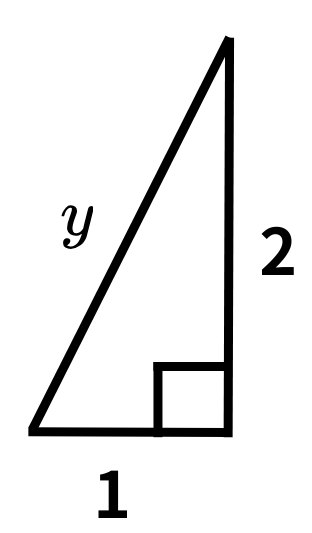

\( y \) を一瞬で求められますか?

\( 1:2:\sqrt{3} \)だから、\( y=\sqrt{3} \)!

よく確認してください。「1と2の間は60°」なのに、今回は90°になっていますね。このときは、三平方の定理に頼るしかありません。間違えやすいので、気をつけましょう!

三平方の定理だから、\( y=\sqrt{5} \) ですね。
まとめ
三角関数の学習は、三平方の定理と有名三角形の理解を土台とします。これらの知識は、与えられた三角比から他の三角比を導く操作や、三角関数を含む方程式・不等式の解法に不可欠です。基礎・基本を丁寧に何度も反復し、辺の比と角の対応をどの向きでも即答できる状態まで確実に定着させましょう。




コメント