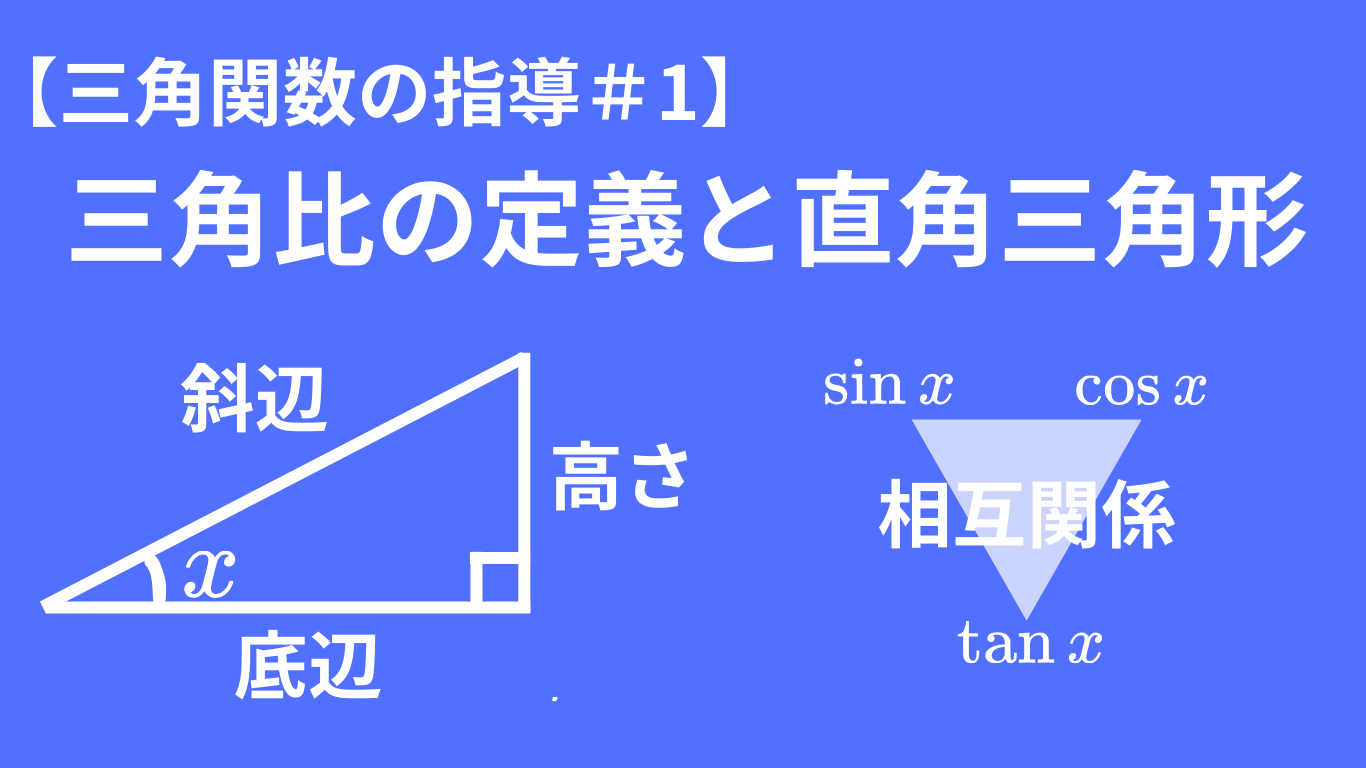
三角関数の学習の基盤は、三角比の定義とその相互関係にあります。三角比の定義は一般角への拡張や三角関数のグラフ理解に直結し、相互関係は式変形や方程式の解法の要となります。特に 「三角比から角度を求める」逆算を正確に扱えるかどうかは、その後の得点率や学習の達成感を大きく左右します。
授業では、生徒の反応を観察しつつ、小刻みな確認 → 即時フィードバック → 再演習のサイクルで繰り返し定着を図ります。
三角比は「直角三角形をかく」から!
数学I「図形の計量」でも数学II「三角関数」でも、私はまず直角三角形を描いて考えることを徹底します。単位円の活用も有効ですが、初学者段階では直角三角形を基盤にした方が、底辺・高さ・斜辺の対応が視覚的に安定し、つまずきを防げると考えています(問題によっては単位円も併用)。
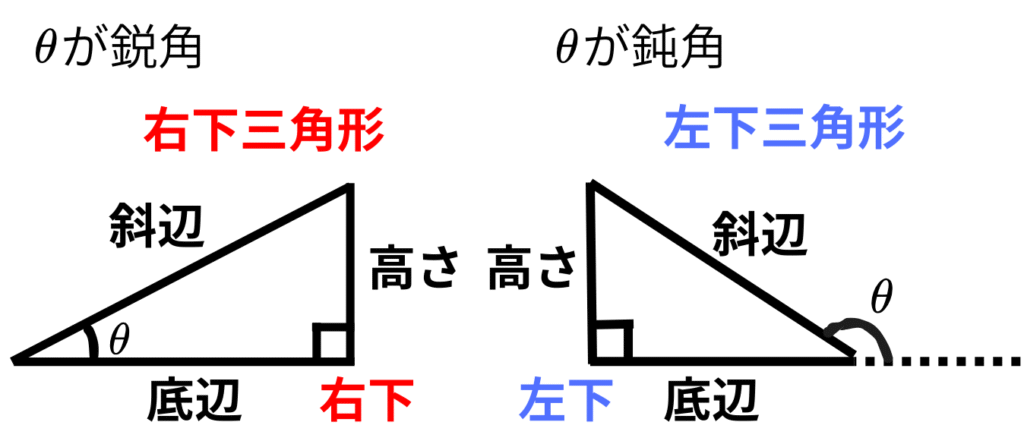
指導手順は 鋭角 → 鈍角 の順。
- 鋭角の三角比では、図は直角を右下に固定してかく。
- 鈍角の三角比では、図は直角を左下に固定してかく。\( \theta \) の位置も確認する。
このように描画の向きを統一することで、生徒は毎回「どこが底辺/高さか」を迷いにくくなり、数学IIでの拡張した三角比・三角関数のグラフにもスムーズに接続できます。
三角比の定義は「底辺・高さ・斜辺」で言語化する
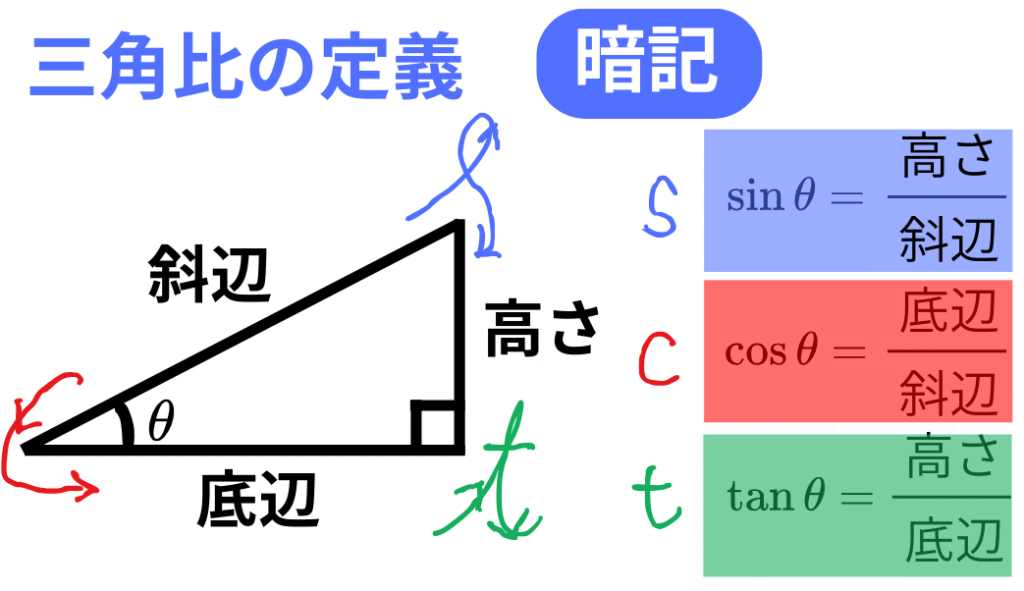
三角比は、図示と言語化の一致で定着します。直角三角形において
\[ \sin\theta = \frac{高さ}{斜辺}, \cos\theta = \frac{底辺}{斜辺}, \tan\theta = \frac{高さ}{底辺} \]
として、\( \sin , \cos, \tan \) を毎回言葉で確認します。繰り返すことにより記憶が安定します。
まずは 鋭角 \( \theta \) で定義を確認し、その後に 鈍角 へ拡張します。鈍角では「辺の長さは常に正」ですが、
底辺をマイナスとして扱う
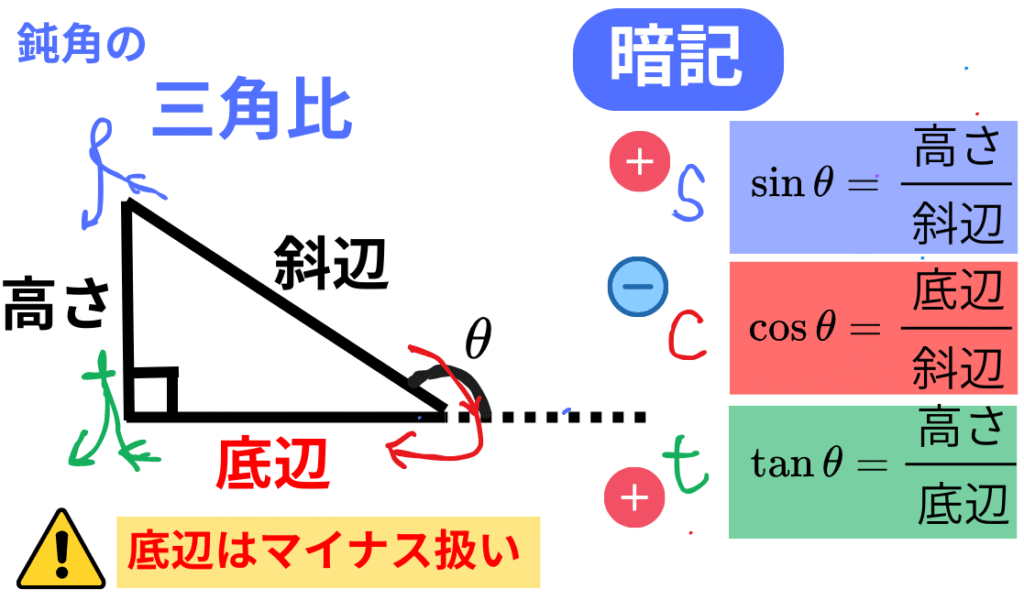
鈍角の拡張は単位円を使うのが一般的ですが、初学者には情報量が多く負荷になりがちです。まずは直角三角形で基準角を描いて符号だけ付加し、最後に三角比の定義によって確認する流れが有効です。大切なのは、矛盾なくwell-defined(整合的)に定義できていることです。
演習による定着
三角比の知識は、演習によって定着していきます。実際に3種類の問題を確認していきましょう。
問題1(与えられた直角三角形の三角比)
この三角比を求めてみましょう。
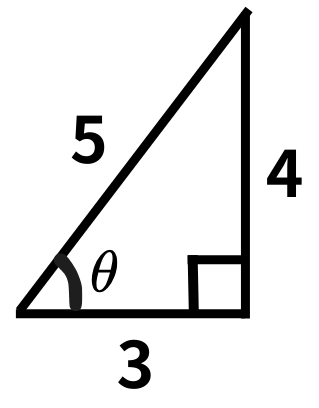
直角三角形において
\[ \sin\theta = \frac{高さ}{斜辺}, \cos\theta = \frac{底辺}{斜辺}, \tan\theta = \frac{高さ}{底辺} \]
となります。
底辺、高さ、斜辺を確認します。
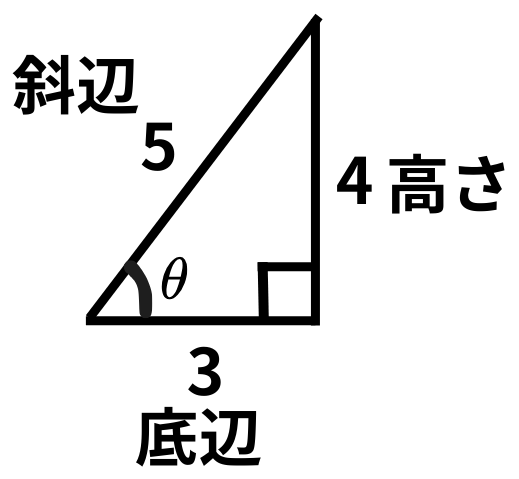
\[ \sin\theta = \frac{4}{5}, \cos\theta = \frac{3}{5}, \tan\theta = \frac{4}{3} \]
問題2(有名角の三角比)
\( \sin45° \)を求めましょう。
・\( \sin \)(三角比)を求めるときは、直角三角形!
・\( 45° \)(鋭角)なので、右下三角形をかく。
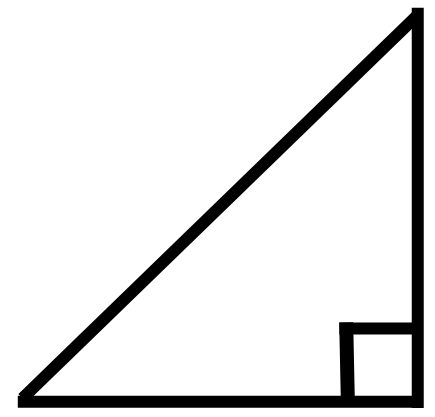
・\( \theta \) を書き入れる
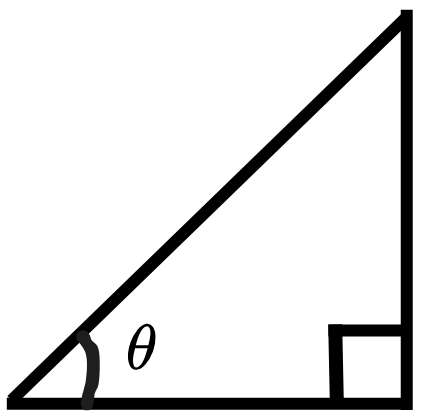
・\(90°, 45° \)なので、\(1:1:\sqrt{2} \)を書き入れる。
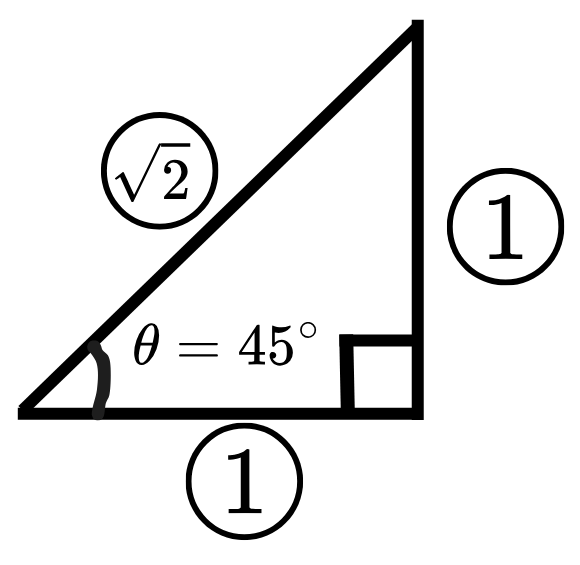
・底辺、高さ、斜辺を確認して求める。
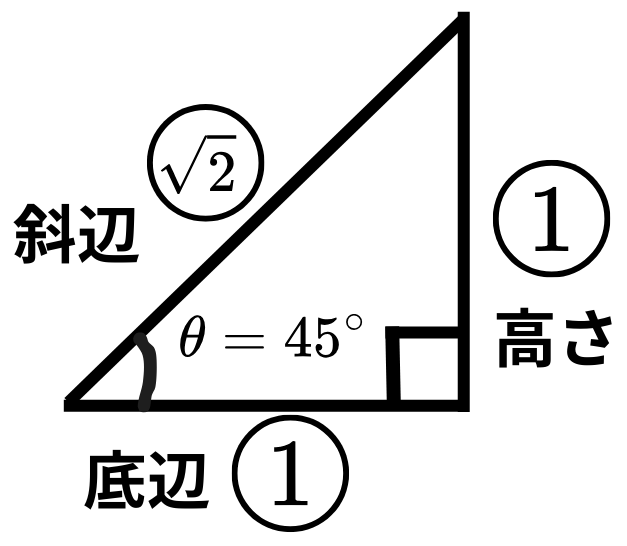
\[ \sin45° = \frac{1}{\sqrt{2}} \]
\( \cos120° \)を求めましょう。
・\( \sin \)(三角比)を求めるときは、直角三角形!
・\( 45° \)(鋭角)なので、右下三角形をかく。

・\( \theta \) を書き入れる
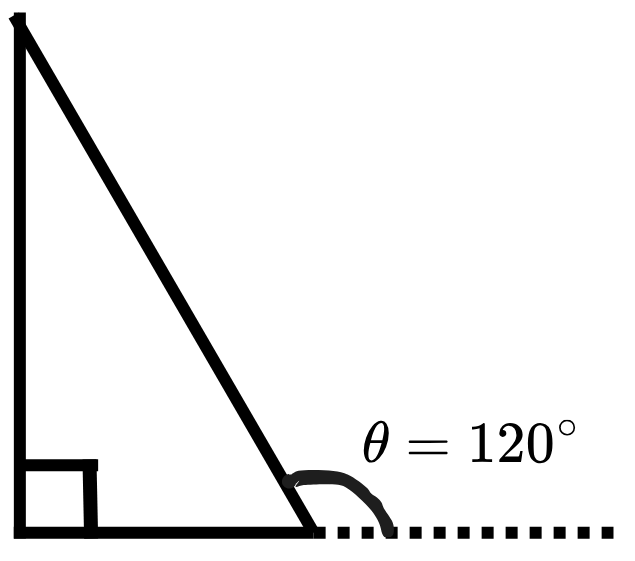
・\(90°, 60° \)なので、\(1:2:\sqrt{3} \)を書き入れる。
※ただし、底辺はマイナス扱い
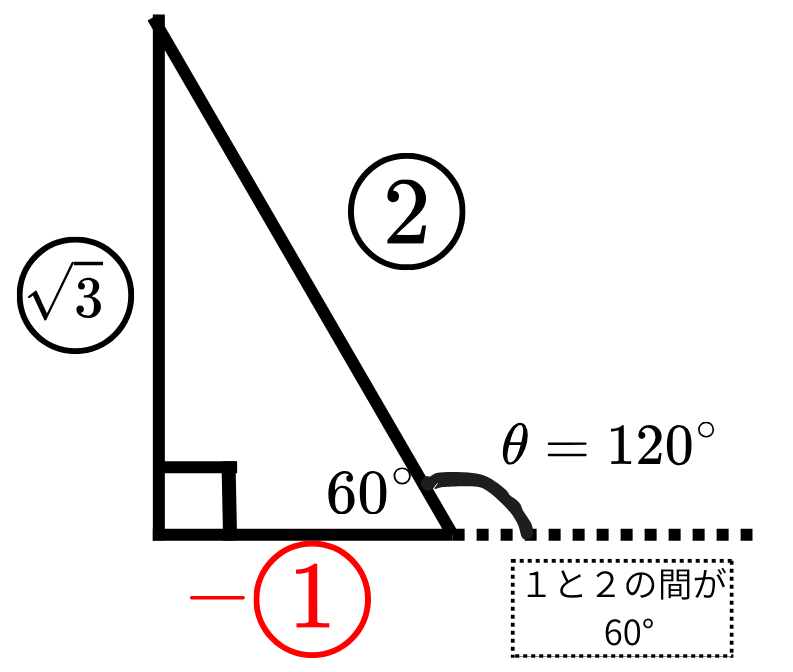
・底辺、高さ、斜辺を確認して求める。
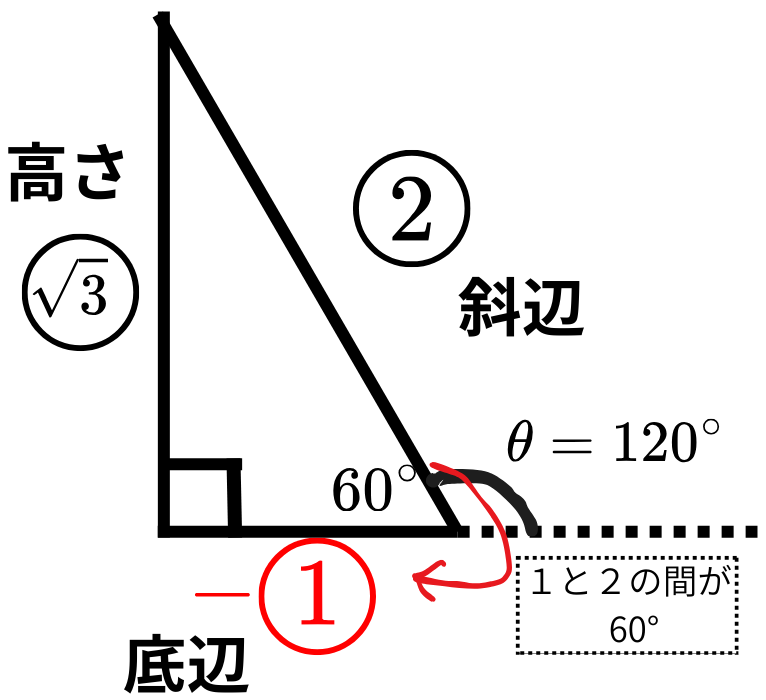
\[ \cos120° = – \frac{1}{2} \]
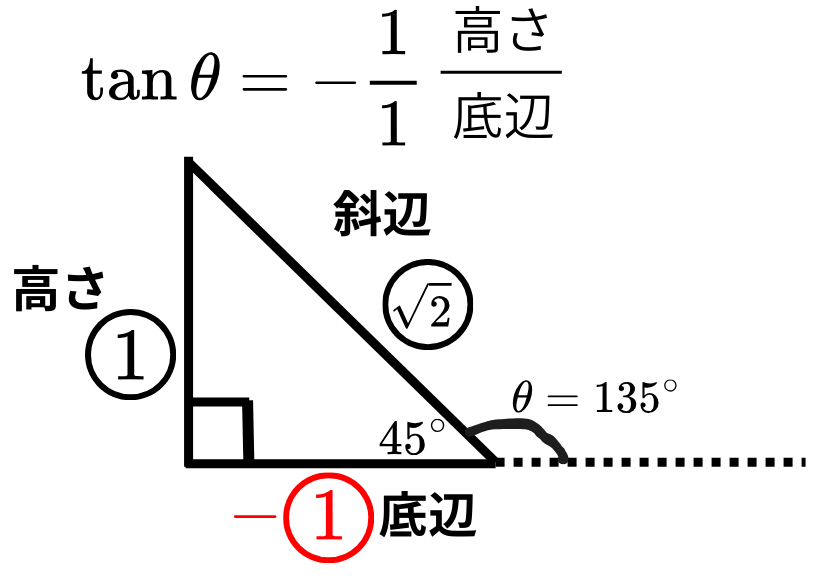
問題3(三角比から角度を求める)
\( 0° ≦ \theta ≦180° \) のとき、
\( \tan \theta = -1 \)を求めましょう。
・\( \tan \)(三角比)を求めるときは、直角三角形!
・\( \tan \)なので、図は1つ。
・\( -1 \)(負の数)なので、鈍角の右下三角形をかく。
・底辺、高さ、斜辺を確認して、図に書き入れる。
・\(1:1:\sqrt{2} \)なので、\(90°, 45° \)を書き入れる。
※ただし、底辺はマイナス扱い
・\( \theta \)の位置に気をつけて、求める。
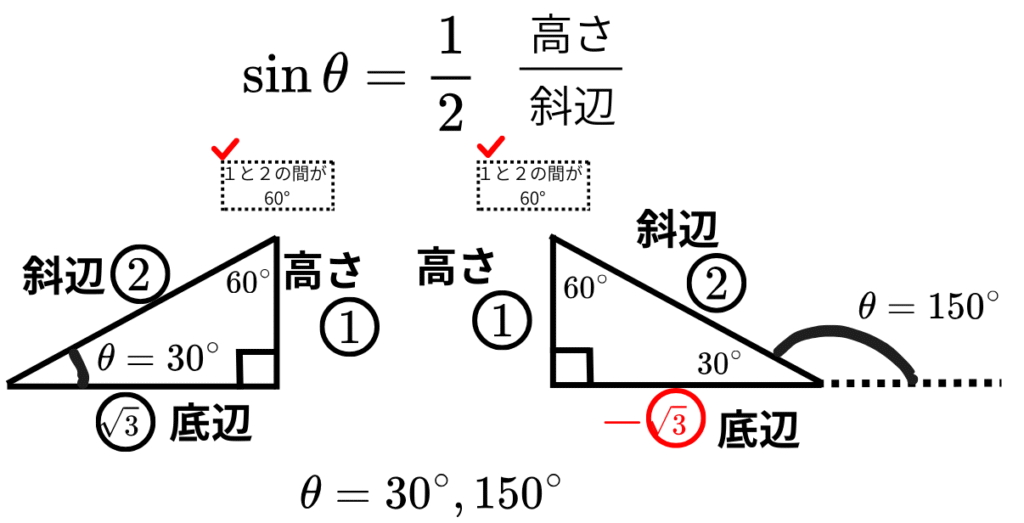
\( 0° ≦ \theta ≦180° \) のとき、
\( \sin \theta = \frac{1}{2} \)を求めましょう。
・\( \tan \)(三角比)を求めるときは、直角三角形!
・\( \sin \)なので、図は2つ。
・鋭角の右下三角形と鈍角の左下三角形をかく。
・底辺、高さ、斜辺を確認して、図に書き入れる。
・\(1:2:\sqrt{3} \)なので、\(90°, 30° \)を書き入れる。
※ただし、底辺はマイナス扱い
・\( \theta \)の位置に気をつけて、求める。
三角比の相互関係

三角比の相互関係は、は、比の変換・因数分解・二倍角の導出などで頻出です。次章以降の加法定理・倍角・三倍角でも土台として繰り返し用います。



コメント