■ はじめに|直線束とは?
高校数学Ⅱ「図形と方程式」では、2つの直線をパラメータで結ぶ“直線束という概念が登場します。教科書によっては扱われないこともありますが、2つの円の共有点を求めるときなどに本質的に用いられる重要な考え方です。
しかし、生徒にとっては初めて触れる抽象的な概念であるため、その理論や意義を理解するのが難しい内容でもあります。
今回は、生成AI「Copilot(Microsoft Bing)」を活用して、2つの直線の交点を通る直線の集合に関する数学的活動を行いました。具体的な図形のイメージとAIによる言語的支援を組み合わせることで、生徒がより深く概念を捉えることを目指しました。
学習指導要領においては、数学科の目標の一つに「主体的に学ぶ態度」の育成が掲げられており、次のように述べられています。
数学的な見方・考え方を働かせ,数学的活動を通して,数学的に考える資質・能力を次のとおり育成することを目指す。
(中略)
(3)数学のよさを認識し,積極的に数学を活用しようとする態度,粘り強く考え,数学的論拠に基づいて判断しようとする態度,問題解決の過程を振り返って考察を深めたり,評価・改善したりしようとする態度や創造性の基礎を養う。
本記事では、こうした指導の意図に基づき、授業の構成と生徒の反応、そしてAIを活用した学びの可能性とその限界について紹介します。
■ 授業の流れと生徒の反応
① 一般的な理論から導入
授業の導入では、やや高校数学の範囲を超える内容ではあるものの、「2つの曲線の共有点をすべて通る曲線」という観点から、以下のような一般式を紹介しました。
2曲線\( f(x,y)=0, g(x,y)=0 \) に対して、
ある点\( (x_0, y_0) \) が\( f(x_0,y_0)=0, \) および \( g(x_0, y_0)=0 \)を満たすとき、
任意の\( s、 t \)に対して, $$ sf(x,y)+t g(x,y)=0 $$ は、2曲線\( f(x,y)=0, g(x,y)=0 \) の共有点をすべて通る曲線を表す。
この式が示すのは、\(s\)や\(t\)の値を任意に変えることで、2つの曲線の交点を必ず通る“新たな曲線”が得られる」という性質です。
理論的には非常に美しく、直線に限らず一般の曲線同士の交点を捉える強力な方法論ですが、実際にこの話をしたところ、生徒たちの表情にはやや戸惑いが見られました。
② 具体的な2直線に限定生徒の反応:良好)
次に、以下の2直線を取り上げ、直線束の具体的な形を確認しました:
- \(L1:2x−y−3=0\)
- \(L2:x+2y−4=0\)
これらをもとに、直線束の方程式 $$ 2x−y−3+k(x+2y−4)=0 ……(1) $$
を導入しました。
このとき、生徒にはまず「式 (1) が 定数 \(k\) に関する恒等式である」ことに着目させ、その共有点を求めることで、どの直線も共通して通る点が存在する(=直線の束である)ことを確認させました。
さらに、式 (1) を展開・整理することで、それぞれの \(k\) に対して直線の一般形が得られることを示すと、生徒たちも納得してくれる様子が見られました。
一方で、「\(k\) の値によって直線が連続的に変化していく」というイメージを持つことは難しかったようで、「何がどう変わっているのか」「なぜ束になるのか」という点については、依然として抽象的な印象を拭いきれない生徒もいました。
■ Copilotに聞いてみた!AIとの協働的学び
ここでCopilotの登場です。全面のスクリーンに、Copilotの画面を投影して
「\( 2x-y-3=0, x+2y-4=0 \) に対して、方程式
\( 2x-y-3+k(x+2y-4)=0 …①\)
を考える。ただし,kは定数である。
①は、どのような図形を表しているだろうか。」
Copilotの回答は、



(2025年6月の実践です)
生徒たちは

よくわからない用語で答えてくるな

でも、先生の説明の通りになっているね。
と、AIの正確さと説明の難しさの両方を実感していました。

せっかくなので、Colipotに質問してください。
生徒に協力してもらって、質問を考えてもらいました。

非常に愛らしい質問をしてくれて、ほっこりしました。表示されたグラフを確認すると…
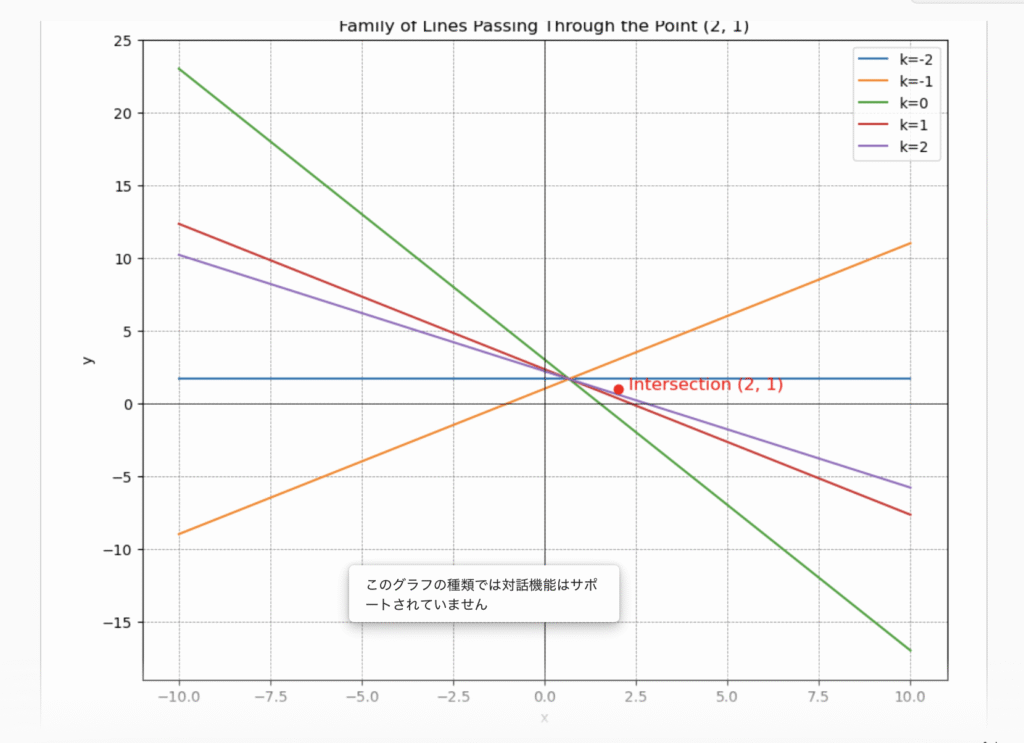
(2025年6月の実践です)

なるほど、直線がたくさんでできるのか。

でも、交点(2、1)が通ってないよね。
生徒たちの会話を聞きながら、理解が深まっているのを感じれました。さらに、修正するように指示すると…

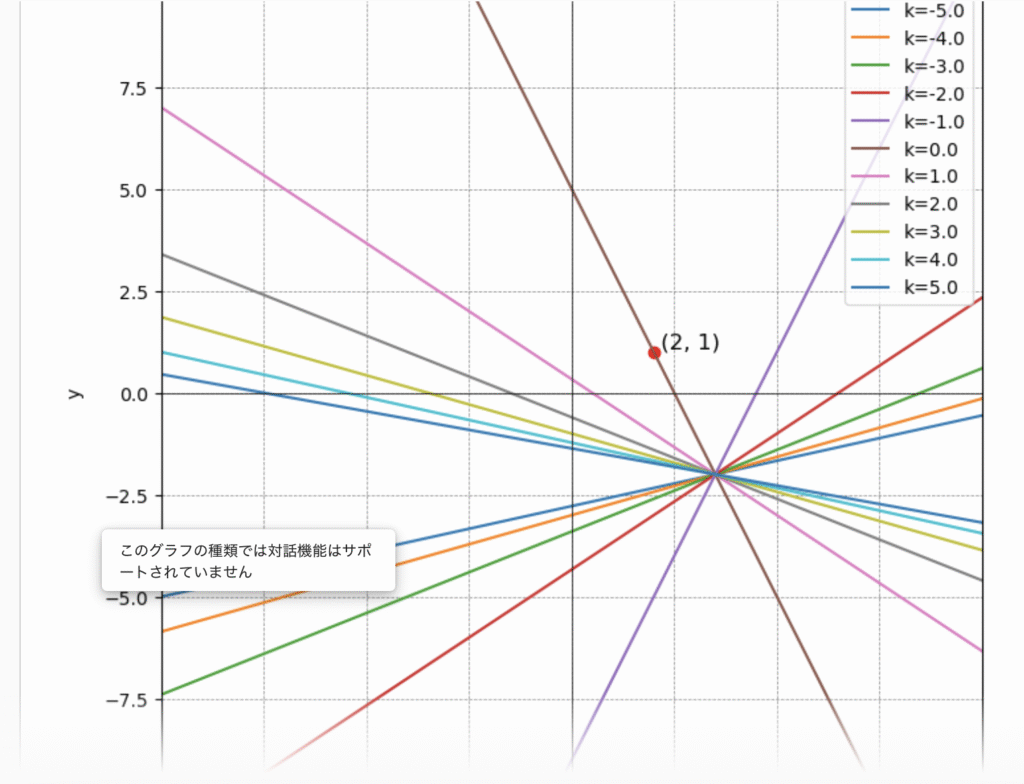
(2025年6月の実践です)

どういうこと?ああ、またエラーで出るんだ!
そのやり取りをしながら、生徒と楽しいやり取りができた授業となりました。
■ Copilotの強みと限界
◎ 良かった点
- 難しい式も瞬時に分類(線形結合や直線束の説明)
- グラフの可視化が容易
△ 限界・注意点
- 説明がやや専門的(生徒向けには難しい)
- 描画の精度が完璧ではなく、交点を通っていないように見える場合も
このように、AIは“完璧な教師”ではないが、頼れるアシスタントになり得る存在であることが、生徒にも伝わったようでした。
■ まとめ|Copilot×直線束=探究の可能性
この実践で生徒たちは、
- 数式の意味を図形でとらえる力
- 直線の集合に共通点を見つける思考
- AIとの対話による新しい学びのスタイル
を体験できました。
AIは「教えてくれる存在」ではなく、「ともに考える存在」
これからも、生成AIと人間が協働する学びのスタイルが、数学教育を豊かにしていくことでしょう。




コメント